 Bingo is a fascinating game. Despite the simple underlying concept there are now many different types of games you can play and this has exploded since online bingo became a thing. 36-Ball bingo is one of the more modern incarnations of the game and is designed a little bit like 30-Ball bingo, often called speed bingo, to be a faster paced game.
Bingo is a fascinating game. Despite the simple underlying concept there are now many different types of games you can play and this has exploded since online bingo became a thing. 36-Ball bingo is one of the more modern incarnations of the game and is designed a little bit like 30-Ball bingo, often called speed bingo, to be a faster paced game.
The 36-Ball game lends itself to specific themes such as Cash Cubes or Fluffy Favourites. You will often recognise the branded names of the games as opposed to them being referred to as 36-ball, but ultimately all these games are based on the same concept. There is usually only one prize with this game for a full house but there are often other prizes and jackpots associated with playing the game over a longer period, e.g. with Cash Cubes you can win prizes for collecting 50 of the same coloured cube.
Being a more simple version of bingo compared with the popular 90-ball or 75-ball variations you would probably think that there are a limited number of possible cards you could produce for a 36-ball game. You would be completely wrong if you thought that as despite the basic concept there are in fact over 37 quadrillion possible card combinations you can produce. Written down that looks like:
37,472,226,311,520,000
That’s any idea of cheating that way out of the window then! Surprisingly due to the layout of the card there are actually far more possible 36-ball cards compared with 30-ball bingo (1,728,00) and 40-ball bingo (4,100,625). It even surpasses the number of 50-ball combinations (just under 6 billion) and astonishingly there are more potential 36-ball cards than there are with 90-ball bingo (24 quadrillion), which is paradoxical when you consider there are 54 extra balls in that game. Only 80-ball and 75-ball bingo have more possible unique cards you can produce.
To give you an idea of how big the number is we are talking about let’s say we use a powerful computer that could generate one million unique 36-ball cards in a single minute. Even then it would take over 71,294 years just to create the maximum number of unique cards.
If you want to know how we worked that number out then read on below.
36-Ball Bingo Card Combinations

How many bingo cards are there?
That’s an interesting question, but a solvable one, with a bit of mathematics!
Each card has 12 numbers, which together create four squares – called ‘cubes’ in the game. The ‘inner’ four numbers on a card each appear in two cubes and the ‘outer’ eight numbers are in only one cube each.
The winner of the game is the one who matches all four cubes, i.e. all 12 of their numbers. However, there are also small bonus payouts available by completing cubes during the course of several games. Therefore even two cards with the same numbers could be different from an overall gameplay perspective based on which numbers are grouped together into cubes on each card.
In order to calculate the number of cards, we need to calculate the number of possible layouts of 12 numbers from the 36 possibilities into the cube layout. Then, we need to make an adjustment for some cards which will exist in this calculation which are identical for gameplay purposes.
Part 1: How many possibilities are there for one column?
The card contains 12 numbers, selected from 36 possibilities. Each number can appear only once on the card.
On a 36-ball bingo card, the layout of the numbers is significant: for example, a card with the numbers 4, 11, 2 and 15 around the first cube is different from one with 8, 11, 2 and 15 around the first cube and the number 4 elsewhere on the card.
This means that we are not just interested in the number of combinations of 12 numbers from 36, but the number of permutations.
Using the standard mathematical formula for the number of permutations without replacement…
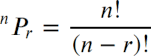
(where n is the number of possibilities and r is the number of selections we are making, i.e. in our case n = 36 and r = 12), we are able to calculate that there are 599,555,620,984,320,000 different permutations of numbers for a single 36-ball bingo card.
Part 2: How many possibilities are there for the entire card?
Whilst we have just calculated that there are a staggering number of possible layouts of numbers on a 36-ball bingo card, in reality some of these cards are functionally identical to one another: the eight numbers around the outside of the card are less important than the four inside numbers because each outside number is only part of a single cube. This means for example that a card with the numbers 11 and 8 on the outside of the first cube and 15 and 32 on the inside, is identical to one with 8 and 11 on the outside and 15 and 32 inside.
In total, there are 2 different possibilities of laying out the outside of each of the four cubes which are identical from a gameplay perspective. This means that for a set of numbers that could appear on the card, there are 2 x 2 x 2 x 2 = 16 total possibilities in the calculation we made in part 1 which would produce an identical game result.
Therefore we need to divide our result from part 1 by 16 to get the number of truly unique 36-ball bingo cards.
599,555,620,984,320,000 ÷ 16 = 37,472,226,311,520,000
Over thirty seven quadrillion!
Python Code Used For The Calculations
Below is the Python code for calculating this, following the same steps as described above.
from math import perm
def total_possible_cards(
possibilities: int,
inside_numbers: int,
outside_numbers: int,
) -> int:
"""
Calculate the total number of different possible 36-ball bingo cards.
"""
cubes = outside_numbers / 2
dupes = 2 ** cubes
return int(perm(possibilities, inside_numbers + outside_numbers) // dupes)
total_possible_cards(
possibilities=36,
inside_numbers=4,
outside_numbers=8,
)37472226311520000