 Games come and go very quickly with 40-ball bingo given you only need to get 8 numbers for a full house, four for a line or four squares (left or right). The nature of the game also means it lends itself to different themes, for example, it is common to see things like four leaf clovers used to represent the four squares on each side.
Games come and go very quickly with 40-ball bingo given you only need to get 8 numbers for a full house, four for a line or four squares (left or right). The nature of the game also means it lends itself to different themes, for example, it is common to see things like four leaf clovers used to represent the four squares on each side.
The symmetry of 40-ball compared to 50-ball means there are three ways to win instead of two and the fast pace of the game means it is popular with people who want to play quick games. You actually need to get less numbers to win with 40-ball compared to the smaller version 30-ball.
Given there are only 40 numbers in this game and eight numbers on a card you must be thinking surely it is possible to buy all the possible tickets in a given game or if playing a real-life game print out all the tickets before and then grab the relevant winning ticket after the minimum number of balls?
Well, it turns out this would not be practical at all because appearances can be deceptive, in reality it turns out there are over 4 million (4,100,625) possible unique combinations of numbers.
Let’s say for some reason you decided you were going to buy every ticket possible for a 40-ball game, how much would this cost? Well, even at 5p a ticket it would set you back £205,031.25.
Should someone decide they wanted to play a real life version of 40-ball and print out the tickets in advance so they could cheat and show the winning ticket after the minimum number of balls are drawn then this would be equally impractical. Should you print one ticket a second it would take you forty seven and a half days of solid printing to do that. The printing costs alone would massively outweigh the potential winnings from cheating.
Read on below to see how we got to this number.
40-Ball Bingo Card Combinations
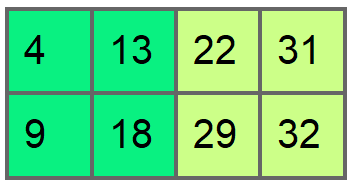
How many bingo cards are there?
That’s an interesting question, but a solvable one, with a bit of mathematics!
Each card has 8 numbers, split into 2 halves. Each half has two columns which each select from a quarter of the possible numbers (so e.g. if number 17 is present on a card, it will always be in the second column, and therefore in the left half of the card).
This means that each column in the card is effectively independent of the others: two cards could have identical first columns, but be different in the other columns. This means we can calculate the number of different possible cards by calculating the different possibilities for each column, and multiplying the results together.
Part 1: How many possibilities are there for one column?
Each column of a 40-ball bingo card contains 2 numbers. These numbers are selected from 10 possibilities: for example, the first column can contain any two numbers from 1 to 10 inclusive.
In 40-ball bingo, the numbers in a given column are always in ascending numerical order. Therefore there is only one way of picking e.g. 13 and 18 in the second column (there’s not a second layout with the 18 above the 13).
Because there is only one ordering for each column, we’re interested in the number of combinations of 2 numbers from 10. We can use the standard mathematical formula for the number of combinations:
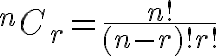
(where n is the number of possibilities and r is the number of selections we are making, i.e. in our case n = 10 and r = 2). Using this formula, we’re able to calculate that there are 45 possibilities for numbers for a particular column.
Part 2: How many possibilities are there for the entire card?
For each possible arrangement of the first column, the card contain any of the possible arrangements for the second column. And then for each of those possibilities, the card could contain any of the possible arrangements for third column, and finally for each of those possibilities the card could contain any of the possible arrangements for the fourth column.
Therefore, to calculate the total number of possible cards, we multiply together the possibilities for each column:
45 x 45 x 45 x 45 = 4,100,625
Over 4 million!
Python Code Used For The Calculations
Below is the Python code for calculating this – so if you’re planning or playing a slight variety of the game, you could tweak this and see how the total number of cards is affected if e.g. there are 5 numbers in each column instead of 4.
from math import comb, prod
def total_possible_cards(columns: int, numbers_per_column: int, possibilities_per_column: int):
"""
Calculate the total number of different possible bingo cards.
"""
return prod(
comb(possibilities_per_column, numbers_per_column)
for _ in range(columns)
)
total_possible_cards(4, 2, 10)4100625