 The 80-ball game is a little more niche compared with 90-ball and 75-ball variations but it has grown in popularity with the rise of bingo online. Despite having a similar number of balls to both 75 and 90-ball games it has a very different card layout, a perfectly square 4×4 grid. This gives the game more combinations that can win other than just a line, two lines and a full house.
The 80-ball game is a little more niche compared with 90-ball and 75-ball variations but it has grown in popularity with the rise of bingo online. Despite having a similar number of balls to both 75 and 90-ball games it has a very different card layout, a perfectly square 4×4 grid. This gives the game more combinations that can win other than just a line, two lines and a full house.
Depending on the game you play and the payout structure you can win for horizontal, vertical and diagonal lines as well as four corner squares, inner square of 4 numbers, outer square of 12 numbers and of course the full house of 16 numbers.
It is an interesting game and lends itself to different themes, which is why its success has been increased as online bingo has grown. Being a symmetrical 4×4 grid, however, must mean it is more simple and there are not that many different cards you can produce?
Well, if you think that you would be wrong as the layout is deceiving, there are in fact over 182 quintillion different possible unique cards you can produce. The 21 digit number written down in full it looks like: 182,818,479,414,274,560,000. That’s any idea of cheating this way out of the window then!
Surprisingly, perhaps, that is more unique cards than is possible with 90-ball bingo (24 quadrillion) but less than 75-ball bingo which can produce 552 septillion (552 followed by 24 more digits) possible cards. Still, the number of 80-ball bingo ticket combinations is an immense number.
To put it into some context let’s say you wanted to print all of those cards and you could print one card per second. You can print 31,536,600 cards per year, a hell of a lot, but even then it would take you just under 5.8 trillion years to print them. That’s around 420 times longer than the universe has existed.
To see how we go to this incomprehensible number read on below.
80-Ball Bingo Card Combinations
How many bingo cards are there?
That’s an interesting question, but a solvable one, with a bit of mathematics!
Each card has 16 numbers, split into 4 columns which each select from a quarter of the possible numbers (so e.g. if number 31 is present on a card, it will always be in the second column).
This means that each column in the card is effectively independent of the others: two cards could have identical first columns, but be different in the other columns. This means we can calculate the number of different possible cards by calculating the different possibilities for each column, and multiplying the results together.
Part 1: How many possibilities are there for one column?
Each column of an 80-ball bingo card contains 4 numbers. These numbers are selected from 20 possibilities: for example, the first column can contain any 4 numbers from 1 to 20 inclusive.
On an 80-ball bingo card, the order in which the numbers appear is significant and can vary. For example, a card with the numbers 1, 13, 19, 14 in the first column is different from one with the same numbers in a different order – because methods of winning including completing rows, columns, or in some games other shapes (e.g. all four corners or the four inner squares), these two different orderings of numbers in a column will give different results.
All of this means we are not just interested in the number of combinations of 4 numbers from 20, but the number of permutations.
Using the standard mathematical formula for the number of permutations without replacement…
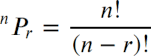
(where n is the number of possibilities and r is the number of selections we are making, i.e. in our case n = 20 and r = 4), we are able to calculate that there are 116,280 permutations for each column.
Part 2: How many possibilities are there for the entire card?
For each possible arrangement of the first column, the card contain any of the possible arrangements for the second column. And then for each of those possibilities, the card could contain any of the possible arrangements for third column. Finally, for each of those possibilities, the card could contain any of the possible arrangements for the fourth column.
Therefore, to calculate the total number of possible cards, we multiply together the possibilities for each column:
116,280 x 116,280 x 116,280 x 116,280 = 182,818,479,414,274,560,000
Over 182 quintillion!
Python Code Used For The Calculations
Below is the Python code for calculating this – so if you’re planning or playing a slight variety of the game, you could tweak this and see how the total number of cards is affected if e.g. there are 12 possible numbers in each column instead of 10.
from math import perm, prod
def total_possible_cards(columns: int, numbers_per_column: int, possibilities_per_column: int):
"""
Calculate the total number of different possible bingo cards.
"""
return prod(
perm(possibilities_per_column, numbers_per_column)
for _ in range(columns)
)
total_possible_cards(4, 4, 20)182818479414274560000