Bingo is a relatively simple game and 30-ball bingo, commonly called speed bingo, is perhaps the simplest of all the game variations.
With only 30 balls to choose from and nine numbers arranged in a 3×3 grid on a ticket surely there are not that many unique combinations of tickets you can make? If you played a real-world game of 30-ball bingo couldn’t you just print out all the possible tickets before the game and produce the correct one after the minimum number of balls have been called?
Well, as it turns out even this very simple bingo game has a very high number of possible combinations, 1.7 million possible unique tickets in fact (1,728,000) and, therefore, you couldn’t possibly pre-print all of the possible unique 30 ball cards before a game.
Given how simple the game is with 30 numbers total and 9 numbers on your card you wouldn’t think there would be that many possible tickets. Even if you printed one ticket per second it would take you 20 days of constant printing just to produce all the possible cards. Assuming you could fit 10 cards on a sheet of paper it would take 172,800 sheets of paper requiring around 17 trees worth of paper to do so. It would cost more in paper and printing to make all the potential unique 30-ball bingo cards than you could win from cheating in a game doing this.
Compared to the number of possible bingo cards for 90-ball or 75-ball bingo 1.7 million is tiny but it is still enough to stop anyone cheating using this method. It would also be uneconomical to buy every possible ticket, even at 5p per ticket it would cost you £84,400 to purchase all the tickets.
If you want to know how we worked that number out then read on below.
30-Ball Bingo Card Combinations
How many bingo cards are there?
That’s an interesting question, but a solvable one, with a bit of mathematics!
Each card has 9 numbers, split into 3 columns which each select from a third of the possible numbers (so e.g. if the number 27 is present on a card, it will always be in the third column).
This means that each column in the card is effectively independent of the others: two cards could have identical first columns, but be different in the other columns. This means we can calculate the number of different possible cards by calculating the different possibilities for each column, and multiplying the results together.
Part 1: How many possibilities are there for one column?
Each column of a 30-ball bingo card contains 3 numbers. The numbers are selected from 10 possibilities: for example, the second column can contain any 3 numbers from 11 to 20 inclusive.
On a 30-ball bingo card, the order in which the numbers appear in a column isn’t significant to your chances of winning. This is because the only way is to win is by a full house. Two cards with the same 9 numbers will win at the same time, even if they appear in a different order. So in these calculations, we won’t be counting two such cards as being different, but just looking for the number of unique cards from a gameplay perspective.
Because we’re not worried about the order, we’re interested in the number of combinations of 3 numbers from 10. We can use the standard mathematical formula for the number of combinations:
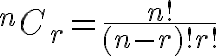
(where n is the number of possibilities and r is the number of selections we are making, i.e. in our case n = 10 and r = 3). Using this formula, we’re able to calculate that there are 120 possibilities for numbers for a particular column.
Part 2: How many possibilities are there for the entire card?
For each possible selection of numbers for the first column, the card could contain any of the possible selections for the second column. And then for each of those possibilities, the card could contain any of the possibilities for the third column.
Therefore, to calculate the total number of possible cards, we multiply together the possibilities for each column:
120 x 120 x 120 = 1,728,000
Over a million, even for this simple form of bingo game!
Python Code Used For The Calculations
Below is the Python code for calculating this – so if you’re planning or playing a slight variety of the game, you could tweak this and see how the total number of cards are affected if e.g. there are only 9 number possibilities for each of the columns.
from math import comb, prod
def total_possible_cards(
columns: int,
rows: int,
possibilities_per_column: int
) -> int:
"""
Calculate the total number of different possible bingo cards.
"""
return prod(
comb(possibilities_per_column, rows)
for _ in range(columns)
)
total_possible_cards(
columns=3,
rows=3,
possibilities_per_column=10,
)1728000